Das Problem und die Idee

Ich lese gerade das wunderbare Buch Elements of Information Theory von Cover und Thomas, um ein bisschen mehr über die Grundlagen der Informationstheorie zu lernen. Das Buch fordert einen von Anfang an recht ordentlich, und man knabbert ein bisschen, bis man alle Beweise durchgearbeitet und verstanden hat. Auf Seite 32 beispielsweise wird das Theorem über die Konvexität der relativen Entropie D(p||q) bewiesen. D.h.:

Für jedes Paar Zufallsfunktionen (p, q) ist die Funktion D(p||q) konvex, wobei D(p||q) definiert ist als:

$$D(p\mid q)=\sum_{x\in X}p(x)*log{\frac{p(x)}{q(x)}}$$

Das wollte ich dann doch einmal mit eigenen Augen sehen, wo da die Konvexität ist! Als Beispiel nehme ich p und q mit nur zwei Zufallswerten an, der allgemeine Fall ist p(0) = r, p(1) =r-1 sowie q(0)=s, q(1)=1-s. D.h. wir ziehen zwei Zufallswerte, wobei der Wert 0 jeweils die Wahrscheinlichkeit r bzw. s hat. Die relative Entropie gibt nun an, wie weit die beiden Wahrheitsfunktionen auseinander liegen, oder anders: wie ineffezient q ist, um p zu beschreiben. Noch informationtheoretischer: wenn man p mit einem Code der durchschnittlichen Länge H(p) (=Entropie von p in Bits) beschreiben kann, aber stattdessen den Code von q benutzt, dann braucht man dazu im Durschnitt H(p)+D(p||q) Bits. Näheres dazu wie gesagt im Buch von Cover und Thomas.

Rechnet man nun D(p||q) für unsere beiden gegebenen Wahrheitsfunktionen aus, dann erhält man:

$$D(p\mid q)=(1-r)*log{\frac{1-r}{1-s}}+r*log{\frac{r}{s}}$$

Diese Funktion wollte ich nun dreidimensional darstellen, und bin nach ein bisschen Googlen auf das Python-Modul Mayavi gestoßen. Das Modul ist ein Teil der äußerst umfangreichen Enthought Tool Suite und enthält u.a. eine GUI zur Darstellung dreidimensionaler Daten und parametrischer Oberflächen. Eigentlich ein bisschen viel für unseren Fall, aber eine andere vernünftige 3D-Plotting-Umgebung konnte ich auf Anhieb partout nicht auftreiben. Wenigstens gibt es Mayavi unter Ubuntu als schönes Paket, wenn man im Paketmanager einfach nach “mayavi” sucht.

Das Paket enthält dann u.a. das Modul mlab, dass man in seinen eigenen Skripten nutzen kann. Eigentlich ist die gesamte Tool Suite als GUI-Anwendung ausgelegt, so liegt dem Ubuntu-Paket beispielsweise die Anwendung “mayavi” bei, über die man Datendateien oder Objekte per GUI betrachten kann. Dazu gibt es dann eine Szene, die die Objekte und zahlreiche weitere Modifikatoren wie Lichtquellen aufnimmt. Diese kann man schön mit Maus und Tastatur modifizieren, drehen, etc. Wir nehmen aber wie gesagt nur das mlab-Modul in einem eigenen Skript. Lustig ist, dass man nach erfolgter Darstellung im eigenen Skript jederzeit zur kompletten GUI umschalten kann. Die GUI wiederum enthält eine Python-Shell, so dass auch der umgekehrte Weg funktioniert. Besonders schön funktioniert das dann mit IPython, womit ich auch das Skript für diese Tutorial entwickelt habe.

Kurz und gut: das fertige Skript sieht folgendermaßen aus:

import numpy
from enthought.mayavi import mlab

[r,s] = numpy.mgrid[0.01:1:0.01,0.01:1:0.01]
d = (1-r)*numpy.log2((1-r)/(1-s)) + r*numpy.log2(r/s)

x = r
y = s
z = d

surface = mlab.mesh(x, y ,z)
mlab.axes()
mlab.show()

Übersichtlich, oder? Zunächst erzeugen wir in r und s die Eingangswerte zwischen 0 und 1 in einem numpy-Grid. Die Funktion der relativen Entropie definieren wir in d. Danach erfolgt die Definition der Koordinaten x, y und z. Hier erlaubt mayavi für jede Koordinate die Angabe einer Funktion, so entsteht dann die Oberfläche des Objekts der Klasse ParametricSurface. In unserem Fall bilden wir die x- und y-Werte einfach auf die Eingangswerte ab, der z-Wert ist dann der Funktionswert. Wir plotten also einfach die Funktion ins Dreidimensional. Schließlich malen wir das Objekt als mesh, fügen noch Achsen per axes() hinzu und zeigen das Ganze per show(), damit sich das Skript nicht gleich beendet und das Ausgabefenster geöffnet bleibt. Es öffnet sich ein Fenster mit unserer Funktion:

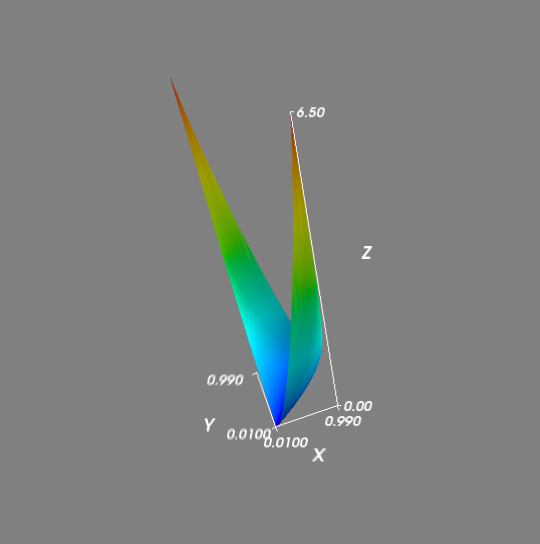
Schön konvex :-) Das Ausgabefenster lädt zum Herumspielen ein, das Objekt lässt sich drehen, Parallelprojektion einschalten und das komplette Mayavi starten, um weitere Daten und Objekte hinzu zu fügen. Oder man arbeitet mit IPython und macht mit der Shell weiter. Viel Spaß!